감염병 예측 모델 (SI, SIS, SIR, SEIR)

SI 모델

SI model 설명1

총 인구수를 N이라고 할때 감염 가능성이 있는 사람의 수를 S(Susceptible)이라고 합니다. 초기에는 S의 값이 N과 비슷하다고 가정하고 하는데 거기에 감염이 시간에 따라서 점점 증가하게 됩니다. 이를 비율로 나타내는 방식을 사용합니다.따라서 $\frac{S}{N}$ 부분이 전체 인구 수 에서 감염 가능성이 있는 사람의 수의 비율부분이 됩니다.

다음으로 감염에 대한 강도라고 하는것은 그 감염병이 얼마나 전파되는지에 대한 beta값과 감염된 사람의 수의 곱의 형태$\beta I$로 표현할 수 있습니다.

$$\frac{dI}{dt} = \beta I \frac{S}{N}$$

감염된 사람이 위와 같이 늘어났으니 시간에 따른 S에 해당하는 수의 변화량은 그만큼 감소하게 됩니다.

$$\frac{dS}{dt} = - \beta I \frac{S}{N}$$

 

SI model 설명2

감염자의 수가 시간에 따라서 어떤 식으로 변하는지를 확인해보기 위해서 식을 정리해주면 결국에 $S+I = N$이므로 $S= N-I$로 볼 수 있습니다.

이를 통해서 $I$에 대해서 적분을 해주면 오른쪽의 식과같이 나오게 되는데 이를 다음에 차근차근 설명해보겠습니다.

 

SI model 설명3

식을 정리하여 $I$와 $t$끼리 양변에 분배해주고 적분을 해주면 미정계수는 T=0일때의 값으로 생각해줄 수 있는데 이경우가 초기 감염된 사람의 수를 바탕으로 얻을 수 있고 이를 정리해주면 $I(t)$를 얻을 수 있습니다.

SI model 설명4

이 식을 잘 살펴보면 Logistic 함수와 같은 꼴로 나오게 되는데 결국 시간이 지남에 따라서 전체 인구수가 감염이 되는 경우로 수렴하는 것을 볼 수 있습니다.

SI model 설명5

이를 시뮬레이션을 해볼 수 있는데 

SI model 시뮬레이션

SI model 설명6

parameter 값에 따른 Intected population 비율

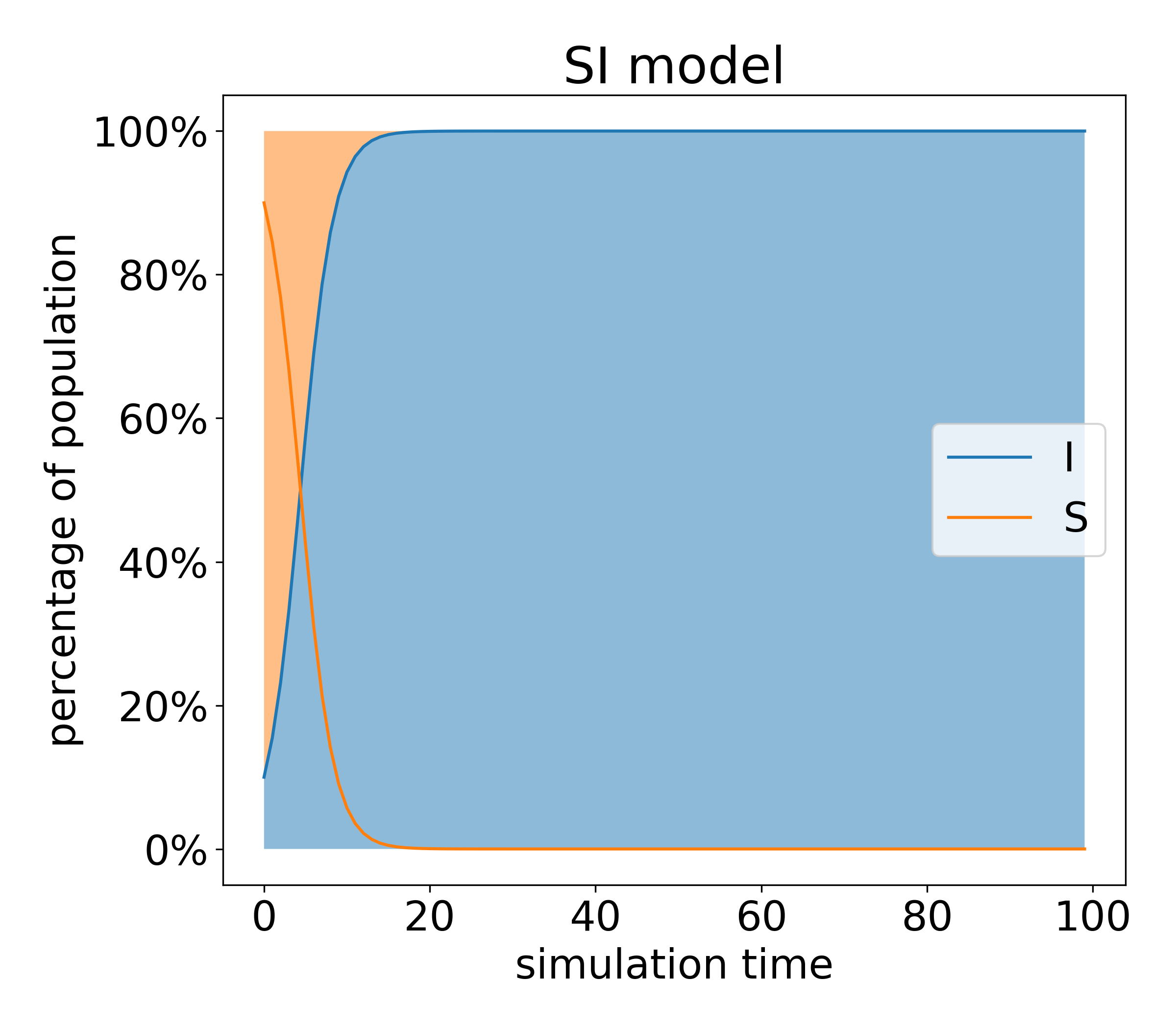
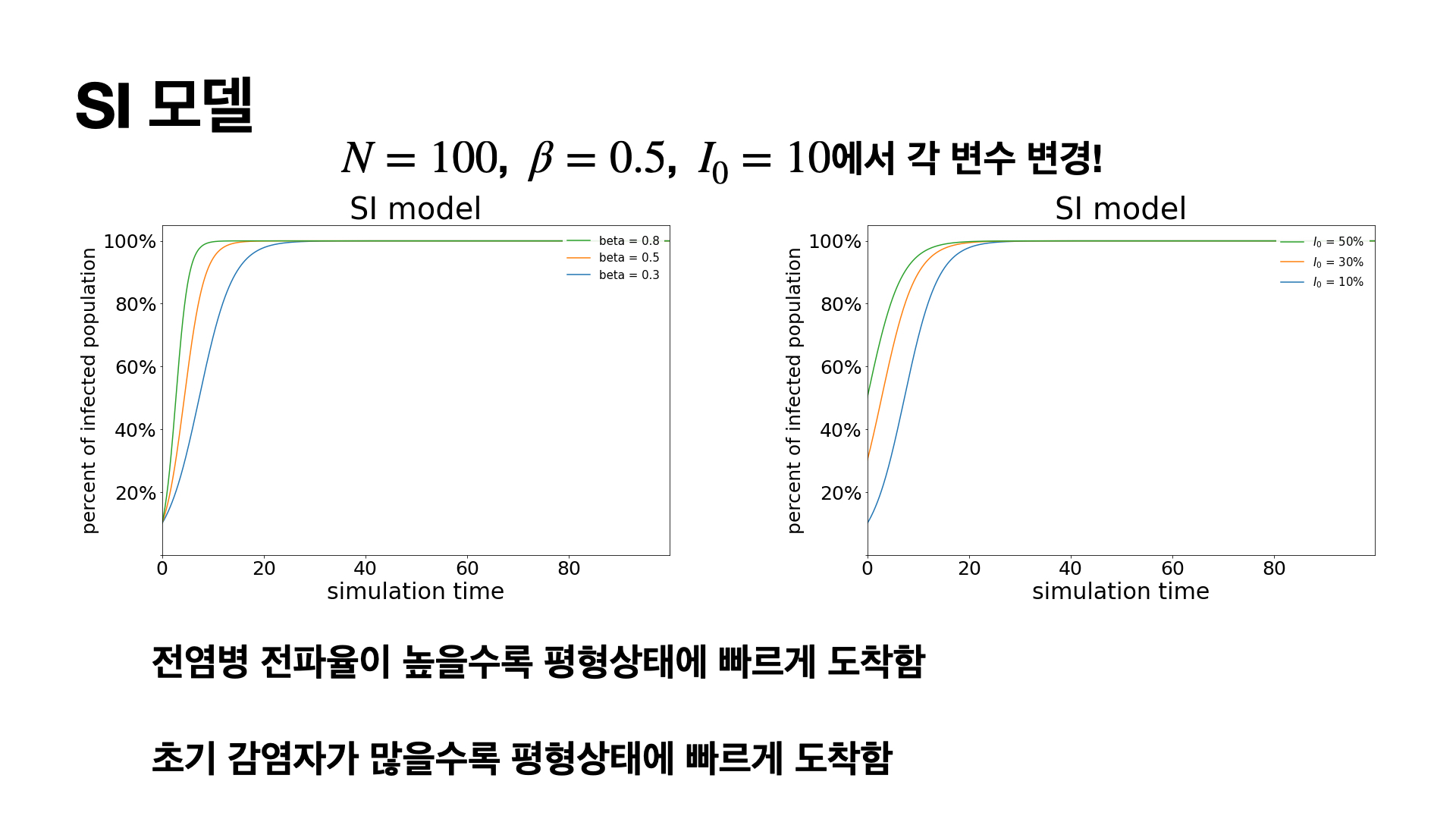
다음과 같이 리프로듀싱을 진행하였습니다.

 

코드는 아래 링크 참고해주세요

https://colab.research.google.com/drive/1QnDvaOxQRgwKA2netA6gDU5QVK3fFJ8I?usp=sharing 

Epidemic_analysis.ipynb

---

 

SIS 모델

SIS model 설명1

이번에는 SIS 모델에 대해서 살펴보겠습니다. 일단 이전 모델과 다른 점은 감염된 사람이 다시 회복해서 감염 가능성이 있는 사람으로 돌아갈 수 있는 경우가 생겼다는 점입니다. 하지만 다시 감염이 될 수 있다는 점이 특징이라고 볼 수 있습니다.

따라서 시간에 따른 S의 변화량에 Infected에서 일정한 확률 $\gamma$만큼 다시 늘어나는 부분이 생기고

그만큼 다시 I의 변화량에 감소하게 됩니다.

 

SIS model 설명2

다시 수식을 풀어줬을 때의 감염자의 수의 함수를 다음과 같이 얻을 수 있습니다. 이를 유도해보겠습니다.

SIS model 설명3

이를 잘 정리해주면 다음과같이 얻을 수 있습니다.

SIS model 설명4

그래프의 경향을 살펴보면 일정 시간동안은 감염자수가 증가하지만 일정 시간이 지나가면 감염자의 수가 일정 비율을 유지하는 것을 살펴볼 수 있습니다. 지금 모델에서 생각해봐야하는 점은 시간이 지나도 감염자수가 사라지지 않고 유지된다는 점입니다.

SIS model 설명5

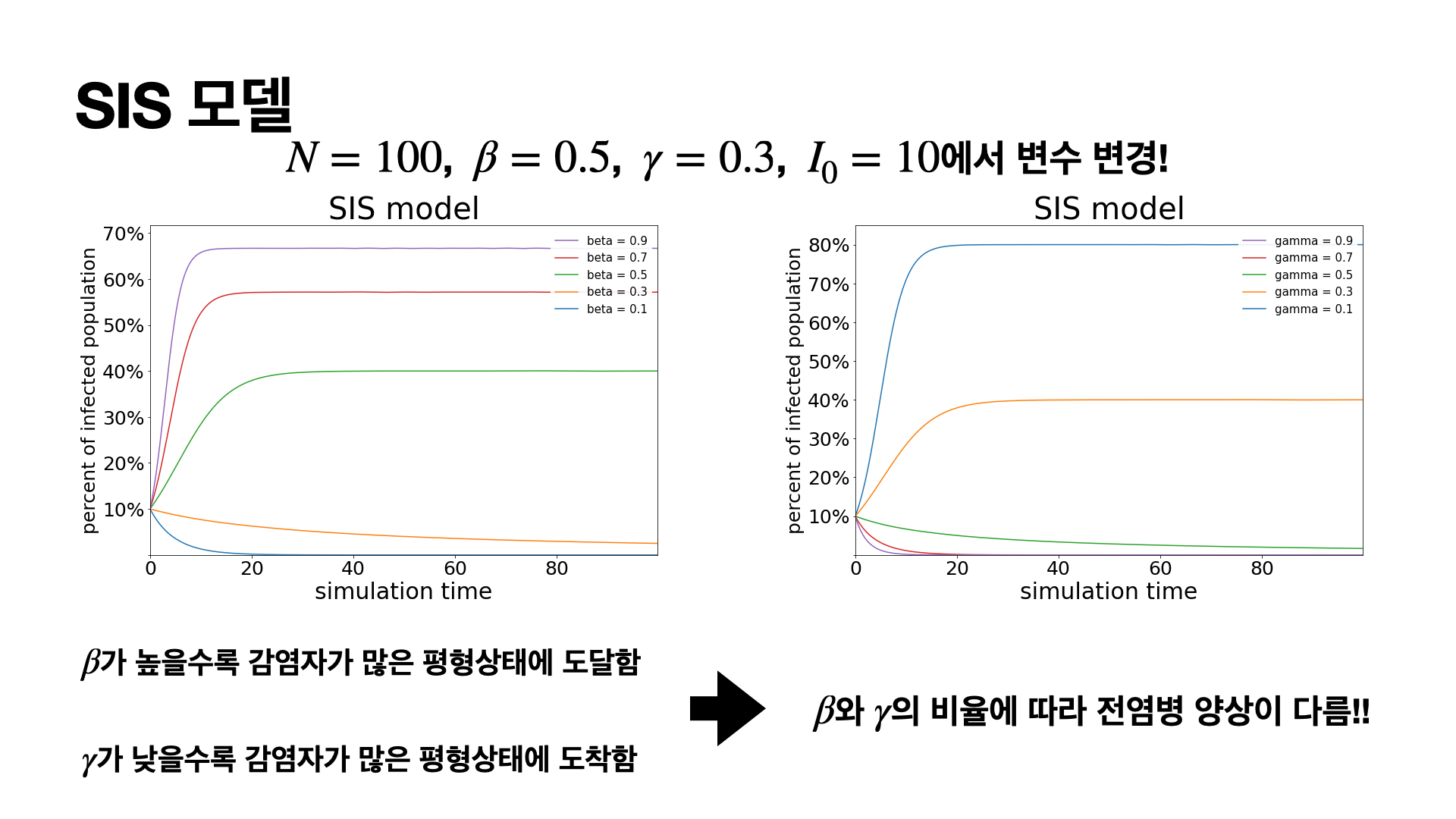
또한 parameter의 값이 달라지는 것에 따라서 어느 값으로 감염자 수가 유지될 것인지에 대해서 변하는 그래프입니다.

 

SIS model 설명6

어떤 감염병이 유행할 것인지에 대한 지표가 되는 것이 기초 재생산 지수라고 할 수 있는데 이 값이 1이하인 경우에는 전염병이 감소하여 종식되는 경우가 되는 것이고 1이상이면 pandemic이라고 해서 감염병이 퍼지는 상황이 됩니다. 코로나의 경우가 초기에 1을 넘는 기초 재생산지수를 가지고 있었기 떄문에 매우 빠르게 확산된 것입니다.

SIS model 설명7

이를 시간에 따라 달라지는 비율에 적용하면 기초 재생산 지수는 시간에 따라 변화하게 됩니다.

---

 

SIR 모델

SIR model 설명1

이전에 살펴본 것이 감염병에서 회복하여 다시 감염가능한 S로 돌아가는 경우였다면 이번에는 면역을 얻어서 병에 걸렸다가 회복된 사람이 다시 병에 걸리지 않는 경우를 살펴볼 수 있습니다. 이렇게 되면 인구를 나누는 기준이 Recovered부분이 하나가 더 생기게 됩니다. 이런 감염병 모델을 만들었을 때 보고싶은 부분은 시간에 따른 감염자의 수를 보고 싶으므로 이를 수식으로 유도하게 됩니다.

SIR model 설명2

여기서는 SIS모델과 같이 $R_e$라는게 중요하다고 보시면 되겠습니다.

SIR model 설명3

이번 모델에서는 면역이라는 것이 적용되어서 감염자의 수가 계속 증가하지 않고 일정 시간이 지나가면 감염자수가 0이되는 경우가 생긴다는 점이 중요하다고 볼 수 있습니다.

SIR model 설명4

$\beta$에 대한 값은 감염발생율에 해당하므로 이 값이 높을수록 감염자의 최대치가 증가하는게 이해할 수 있고, $\gamma$에 대한 값은 회복율에 해당하므로 이 값이 낮을수록 감염자의 최대치가 증가하는게 이해가 됩니다. 

SIR model 설명5

위의 SIS모델에서와 같이 기초 재생산 지수가 나오고 중요한 지표입니다.

SIR model 설명6

추가로 이 기초 재생산 지수는 시간에 따른 인구의 비율의 변화에 비례하여 다른 기초재생산지수를 가질 수 있다. $R_t$

 

출처 <보건복지부 2021.11.15 보도자료 코로나19 백신？치료제 임상시험 지원 강화방안>

 

보건복지수에서 발행한 보도자료를 통해 글작성 시기에 해당하는 감염재생산지수를 살펴보자면 시간에 따라 달라지고 대체로 1을 넘는 값을 가지고 있다는 것을 확인할 수 있다.

http://www.mohw.go.kr/react/al/sal0301vw.jsp?PAR_MENU_ID=04&MENU_ID=0403&page=1&CONT_SEQ=368460 

알림 > 보도자료 내용보기 " 코로나19 백신？치료제 임상시험 지원 강화방안 " | 힘이 되는 평생

 

---

 

SEIR 모델

SEIR model 설명1

지금까지는 감염 가능한 사람이 바로 감염되는 경우를 살펴보았는데 이는 실제는 감염병이 더 많은 사람을 감염시키기위해서 잠복기라는 추가하여 진화하였고 이를 모델에 적용해보는게 더 현실적입니다. 이처럼 바로 증상이 나타나지 않고 잠복기에 머무는 경우가 있기 때문에 이를 보완하기 위해서 모델에 감염병에 노출된 사람의 수(Exposed)를 추가해주었습니다.

또한 잠복기인 사람이 증상이 나타나는 감염된 사람이 되기 까지의 기간에 대한 역수가 $\sigma$입니다. 예를 들어서 코로나의 경우 14일이라고 하면 $\sigma$는 그에 역수인 $\sigma = 0.0714$에 해당하게 됩니다.

SEIR model 설명2

이번에는 감염자뿐만 아니라 잠복기인 사람도 살펴보기 위해서 단순 적분이 아니라 행렬 계산을 해줘야한다.

SEIR model 설명3

전염병이 초기일 때의 감염자의 변화는 지수적으로 증가하는 경향을 보이고

SEIR model 설명4

전염병이 사라지는 말기일 때의 감염자의 변화는 logistic 함수의 꼴로 나타난다.

SEIR model 설명5

 

SEIR model 설명6

SEIR model 설명7

 

 

appendix

1. 장경환 선배님의 모델 정리 자료
2. 위니버스 기초 재생산지수 https://www.youtube.com/watch?v=G-mHyTueAGw 
3. 위니버스 SIR 모델 https://www.youtube.com/watch?v=S4v1xAlLeCI&t=402s

기초재생산지수 참고자료

SIR 모델 참고자료